ANTECEDENTES

La determinación de los parámetros sísmicos se hace de acuerdo a la zona en la que se encuentra ubicada la edificación, de acuerdo a la norma de diseño sísmico E030, además se toma en cuenta el tipo de suelo sobre el que se encuentra asentado, en nuestro caso la estructura se encuentra ubicada en Arequipa, específicamente en Camaná, además el tipo de suelo se clasifico como S3, de acuerdo con estas consideraciones tenemos que el factor de zona y el factor de suelo son 0.45 y 1.10, respectivamente.

La estructura será una universidad, por tanto esta clasifica como una estructura de tipo esencial, además esta usara una combinación de placas y pórticos como sistema resistente frente a cargas laterales, por tanto el factor de uso y factor básico de reducción fueron de 1.50 y 6 respectivamente.

Parámetros sísmicos

z	0.45	Factor de zona: Camaná, Arequipa.
s	1.10	Factor de suelo
Tp	1.00
Tl	1.60
u	1.50	Categoría de la edificación: Universidad
Ro	6.00	Factor de reducción básico
Ia	1.00
Ip	1.00
R	6	Factor de reducción
T	0.29	Periodo de la estructura
C	2.50	Factor de amplificación sísmica

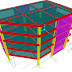
VISTAS DEL MODELO MATEMÁTICO

El modelo matemático usado para la modelación se construyó usando el software SAP 2000, las vistas más importantes del modelo se presentan en la Figura 1 y Figura 2.

PERIODOS FUNDAMENTALES

Los resultados del cálculo de las doce formas de modo se presenta en la Tabla 1, de este grafico podemos ver que la primera forma de modo tuvo un periodo de vibración de 0.453 segundos, mientras que la segunda forma modo tuvo un periodo de 0.413 segundos.

Las formas de modo correspondientes se presentan en la Tabla 5 y en la Tabla 6, de estos gráficos podemos ver que la primera y segunda formas de modos son traslacionales, mientras que la tercera forma de modo resultó ser rotacional.

PESO SÍSMICO DEL EDIFICIO

La determinación del peso del edificio se hizo mediante el programa SAP 2000, en la Tabla 2 se muestran los pesos por niveles y el peso de cada nivel, como podemos ver de esta tabla el peso debido a las cargas muertas fue de 2080.23 t, mientras que el peso de la estructura debido a las cargas gravitacionales fue 446.46 t.

CÁLCULO DE FUERZA CORTANTE BASAL

Este método representa las solicitaciones sísmicas mediante un conjunto de fuerzas estáticas equivalentes actuando en el centro de masas de la edificación.

Parámetros sísmicos

z	0.45		Factor de zona: Camaná, Arequipa.
s	1.10		Factor de suelo
Tp	1.00
Tl	1.60
u	1.50		Categoría de la edificación: Universidad
Ro	6.00		Factor de reducción básico
Ia	1.00
Ip	1.00
R	6		Factor de reducción
T	0.45		Periodo de la estructura
C	2.50		Factor de amplificación sísmica

Peso de la edificación

Wd	2080.23	Ton	Peso debido a la carga muerta
wl	446.46	Ton	Peso debido a la carga viva
W=wd+0.50wl	2303.46	Ton	Peso sísmico

La cortante estática basal se calcula mediante la siguiente expresión:

V=ZUCSW/R

V	712.6	Ton	Cortante estático basal

DISTRIBUCIÓN EN ALTURA

La cortante basal debe ser distribuida en altura, de acuerdo a lo establecido en la norma de diseño sismoresistente, a continuación se muestra el esquema usado en para obtención de las fuerzas laterales de piso.

Nivel	h(m)	Wd(Ton)	Wl(Ton)	Ws(Ton)	wh^k	α	F
1	3.50	424.2	101.5	474.90	1662.14	0.07	50.0
2	7.00	424.2	101.5	474.90	3324.28	0.14	100.0
3	10.50	424.2	101.5	474.90	4986.42	0.21	150.0
4	14.00	424.2	101.5	474.90	6648.56	0.28	200.0
5	17.50	383.6	40.6	403.87	7067.71	0.30	212.6
∑					23689.11	1.00	712.6

RESULTADOS DEL ANÁLISIS

VERIFICACIÓN DE DERIVAS Y DESPLAZAMIENTOS

Las distorsiones máximas por piso se graficaron con la altura de la edificación y se muestran en la Figura 7, de este grafico podemos ver que en todo momento las distorsiones máximas estuvieron por debajo de la distorsión máxima permitida por la norma E030.

VERIFICACIÓN DE IRREGULARIDADES

A continuación se calculan las irregularidades presentes en las estructuras, estas serán calculadas de acuerdo con los lineamientos de la norma E030.

Irregularidades de rigidez-Piso blando

De acuerdo con la norma E030, una estructura presenta irregularidad de rigidez en altura, en específico piso blando, si la distorsión de un nivel es 1.4 veces la distorsión máxima del piso inmediato superior. En la Tabla 3 se presentan los desplazamientos máximos originados por las fuerzas sísmicas en la dirección X y el cálculo de la razón entre las distorsiones en un nivel y el nivel inmediato superior.

Tabla 3: Verificación de la rigidez de piso blando en la dirección X.

Dirección X
Piso	Altura	D.t.e. (m)	d.t.i(m)	d.r.i.(m)	distorsión	Δi/Δi+1	Límite	Obs
1	3.5	0.002286	0.013716	0.013716	0.0039
2	3.5	0.006721	0.040326	0.02661	0.0076	0.515	1.4	Ok
3	3.5	0.012321	0.073926	0.0336	0.0096	0.792	1.4	Ok
4	3.5	0.018352	0.110112	0.036186	0.0103	0.929	1.4	Ok
5	3.5	0.02427	0.14562	0.035508	0.0101	1.019	1.4	Ok

En la se presenta una tabla en la que se presentan los cálculo de las distorsiones inelásticas, de acuerdo a la norma E030, de estos resultados podemos ver que en ningún caso se presentó la irregularidad por rigidez en altura.

Tabla 4: Verificación de la rigidez de piso blando en la dirección Y.

Dirección Y
Piso	Altura	D.t.e. (m)	d.t.i(m)	d.r.i.(m)	distorsión	Δi/Δi+1	Límite	Obs
1	3.5	0.001796	0.010776	0.010776	0.0031
2	3.5	0.005184	0.031104	0.020328	0.0058	0.530	1.4	Ok
3	3.5	0.00947	0.05682	0.025716	0.0073	0.790	1.4	Ok
4	3.5	0.014121	0.084726	0.027906	0.0080	0.922	1.4	Ok
5	3.5	0.018721	0.112326	0.0276	0.0079	1.011	1.4	Ok

Por tanto se obtiene que:

Ia=1.00

Ip=1.00

Irregularidad de peso

La irregularidad en masa se presenta si la masa de un piso es mayor o igual a 1.5 veces la mas del piso inmediato superior, de acuerdo con esto se presenta el cuadro siguiente, en el que se observa que la relación de las masas de un nivel y el inmediato superior es menor a 1.5.

Nivel	Altura	Masa x	Masa y	(Mi/Mi+1)x	(Mi/Mi+1)y	Limite	Obs
1	3.5	224.09	224.09
2	3.5	224.09	224.09	1	1	1.5	Ok
3	3.5	224.09	224.09	1	1	1.5	Ok
4	3.5	224.09	224.09	1	1	1.5	Ok
5	3.5	224.09	224.09	1	1	1.5	Ok

Por tanto se tiene que:

Ia=1.00

Ip=1.00

Irregularidad geométrica vertical

La irregularidad geométrica vertical no aplica en este caso, ya que la relación de las dimensiones correspondientes en todos los niveles es la misma.

Por tanto se tiene que:

Ia=1.00

Ip=1.00

Discontinuidad en los sistemas resistentes

La discontinuidad de los sistemas resistentes no aplica en el caso analizado, ya que como se ve de los modelos presentados existe continuidad vertical de todos los elementos verticales.

Por tanto se tiene que:

Ia=1.00

Ip=1.00

Irregularidad torsional

La estructura en general no presenta irregularidades en altura, ya que existe continuidad en rigidez, en masa y en resistencia, sin embargo podemos ver que existe asimetría geométrica en planta por tanto se realizó la verificación de irregularidad torsional en planta, los resultados se muestran en la Tabla 3.

Tabla 5: Determinación de la irregularidad torsional en planta.

Nivel	drxC.M.	dryC.M.	drxMAX	dryMAX	drMax/drCM	drMax/drCM
1	0.067416	0.059268	0.008724	0.007824	0.129	0.132
2	-0.058986	-0.051678	0.013908	0.012078	0.236	0.234
3	0.013254	0.011694	0.016224	0.013908	1.190	1.189
4	0.015384	0.013488	0.016674	0.01419	1.084	1.052
5	0.015762	0.01377	0.01545	0.013068	0.980	0.949

De los resultados presentados vemos que la estructura no presenta irregularidad en planta, ya que esa condicione exige que el cociente entre los máximos desplazamientos relativos de cada piso sea por lo menos 1.2 veces el desplazamiento del centro de masas de ese nivel.

Por tanto se tiene que:

Ia=1.00

Ip=1.00

Esquina entrante

El caos de esquina entrante no aplica en el caso de la estructura analizada, puesto que no existe la configuración requerida en planta.

Por tanto se tiene que:

Ia=1.00

Ip=1.00

VERIFICACIÓN DEL FACTOR BASICO DE REDUCCIÓN R

El factor de reducción básico de fuerzas sísmicas depende del tipo de sistema estructural elegido, sin embargo la determinación del tipo de sistema estructural no es trivial, ya que los sistemas estructurales se definen por el porcentaje de fuerza sísmica que absorben los elementos estructurales representativos de cada sistema.

En nuestro caso la estructura analizada presenta muros y pórticos de concreto, aunque a priori se especule que se trata de un sistema dual, se deben calcular los porcentajes de fuerza sísmica que absorben las placas y los pórticos y determinar de manera precisa el tipo de sistema estructural.

Tabla 6: Fuerzas en columnas inducidas por el sismo Qx.

Elemento	Sismo	Axial(t)	V2(t)	V3(t)	T(t.m)	M2(t.m)	M3(t.m)
33	Qx	-11.67	3.83	-0.15	0.03	-0.43	10.75
102	Qx	277.87	4.79	-0.23	0.03	-0.32	11.82
127	Qx	-277.77	4.79	0.24	0.03	0.35	11.82
132	Qx	13.05	3.82	0.16	0.03	0.45	10.74
137	Qx	20.63	3.50	-0.11	0.03	-0.38	10.19
142	Qx	3.08	4.75	-0.44	0.03	-0.55	11.59
147	Qx	-6.68	4.74	0.25	0.03	0.36	11.57
152	Qx	-21.76	3.81	0.10	0.03	0.38	10.54
157	Qx	287.94	4.45	0.12	0.03	-0.13	11.06
162	Qx	-281.38	4.76	-0.23	0.03	-0.33	11.41
167	Qx	-16.02	4.37	-0.28	0.03	-0.23	10.97

En la Tabla 3 se presenta un resumen de las fuerzas internas inducidas en la columnas de concreto de la estructura debido al sismo en la dirección x (Qx), de la misma manera en la Tabla 4 se presenta un resumen de las fuerzas sísmicas inducidas en las columnas por el sismo aplicado en la dirección y (Qy).

Tabla 7: Fuerzas en columnas inducidas por el sismo Qx.

Elemento	Sismo	Axial(t)	V2(t)	V3(t)	T(t.m)	M2(t.m)	M3(t.m)
33	Qy	268.77	-0.27	4.27	-0.02	10.55	-0.44
102	Qy	-0.60	-0.16	3.26	-0.02	9.30	-0.31
127	Qy	9.24	-0.06	3.19	-0.02	9.12	-0.20
132	Qy	254.16	0.11	4.02	-0.02	9.92	-0.01
137	Qy	-263.95	0.09	4.53	-0.02	10.84	0.09
142	Qy	-3.12	0.19	4.23	-0.02	10.38	0.20
147	Qy	-2.90	-0.18	4.12	-0.02	10.16	-0.21
152	Qy	-252.95	-0.49	4.10	-0.02	10.00	-0.56
157	Qy	0.28	0.11	3.66	-0.02	9.87	0.24
162	Qy	-7.84	0.10	3.23	-0.02	9.27	0.22
167	Qy	-11.39	-0.25	3.60	-0.02	9.57	-0.17

En la Tabla 5 se presenta un resumen de las tablas presentadas anteriormente, en esta tabla se presenta únicamente las fuerzas cortantes debidas a los sismos presentes en X e Y, de estos resultados vemos que el porcentaje de fuerzas cortantes absorbidos por las columnas suman un total de 47.62 t y 42.23 t en las direcciones x e y, respectivamente.

Además de acuerdo a los cálculos anteriores el cortante basal inducido por el sismo de diseño fue de 712.6 t, por tanto las columnas en las direcciones x e y absorben el 6.70% y 5.90% del total de la fuerza sísmica.

De acuerdo con estos resultados los muros de concreto armado están absorbiendo el 93.3% y 94.1% de la fuerza sísmica en las direcciones x e y, respectivamente, por tanto el sistema estructural es de muros de concreto armado, con lo que la suposición inicial fue la adecuada, por tanto.

Rx=Ry=6

Tabla 8: Fuerzas cortantes en columnas debidas al sismo en x (Qx) e y (Qy).

Columna	V/Qx	V/Qy
33	3.83	4.27
102	4.79	3.26
127	4.79	3.19
132	3.82	4.02
137	3.50	4.53
142	4.75	4.23
147	4.74	4.12
152	3.81	4.10
157	4.45	3.66
162	4.76	3.23
167	4.37	3.60
Total	47.62	42.23

CONCLUSIONES

o El sistema estructural predominante fueron los muros de concreto armado, puesto que como se vio estos absorben mas del 90 % del cortante basal, tanto en dirección x, como en dirección y.

o La estructura resultó ser una estructura regular, pues como se vio no presenta irregularidades en altura y en planta, en específico se mostró que la estructura no presenta irregularidad torsional, ya que el parámetro de torsión sólo llego a 1.19.

4 comentarios:

Victor6/07/2018
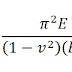
Buenas, la división en la verificación de irregularidad de piso blando esta invertida. Se debe dividir el piso actual sobre el inmediato superior. Tienes irregularidad extrema de piso blando. Saludos.
ResponderEliminar
Respuestas
Unknown9/14/2018
me gustaria que me ayudara con el calculo de la irregularidad por resistencia o piso débil
ResponderEliminar
Respuestas