ANÁLISIS DE UN RESERVORIO CILINDRICO

Preparado por: Eden Capcha M.

Se analizará un cilindro sometido a presión hidrostática, el radio del cilindro es de 3m, la altura del cilindro es de 6.00 m y el espesor del cilindro fue de 0.25 m; el material es concreto con módulo de elasticidad E=2534563.5 Ton/m2.

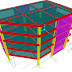
El modelo generado en SAP 2000 se muestra en la Fig. N° 7 , así como las cargas actuantes sobre la estructura, la deformada se muestra en la Fig. N° 8 de donde podemos ver que el valor máximo de la deformada fue de 0.0008 m en dirección radial.

Los esfuerzos (S11 y S22)  en la cara visible se muestran en la Fig. N° 9, de donde podemos observar la variación de estos a lo largo del cilindro, vemos que el valor máximo del esfuerzo S11 fue de 740 Ton/m2 y el de S22 fue de -1267 Ton/m2.

Probablemente sea de mayor interés conocer la variación de las fuerzas circulares F11 y de momentos M22 dentro del cilindro, esto se puede visualizar gráficamente en la Fig. N° 11, donde los máximos valores fueron 140 Ton y de 8.20 Ton.m respectivamente.

 A fin de contrastar los resultados obtenidos se revisa la solución de  la ecuación diferencial que gobierna la flecha producida por carga hidrostática, esta tiene la forma:

.

Suponiendo la lámina como infinitamente rígida y mediante la inclusión de las condiciones de borde, tales como el hecho de que en el fondo la pared de la lámina se encuentra empotrada a una cimentación infinitamente rígida, tenemos la solución para este problema:

A continuación se presentan los resultados de la solución teórica como gráficos de las funciones de interés contra la longitud del eje del cilindro:

En la Fig. N° 12 se puede observar la deformada a lo largo del eje del cilindro, el valor máximo es de aproximadamente 8.m, y de los resultados obtenidos utilizando elementos SHELL(Fig. N° 2)  tenemos un valor de 0.0008, como vemos ambos valores coinciden exactamente.

En la Fig. N° 13 se muestra la variación de la fuerza circular en función del eje del cilindro, de este podemos ver que el valor máximo se obtuvo aproximadamente a 1.5 m de la base con un valor aproximado de 137 Ton.m, mientras que el valor obtenido usando elementos SHELL fue de 140 Ton.m aproximadamente.

En la Fig. N° 14 se muestra la variación de momentos flectores en función del eje del cilindro, como podemos ver del gráfico adjunto el momento máximo ocurre en la base del cilindro y da como resultado un valor de 9 Ton.m, mientras que el momento máximo obtenido mediante la utilización de elementos SHELL tuvo un valor de 8.2 Ton.m.

CONCLUSIONES

La solución obtenida mediante el uso de elementos SHELL y la malla mostrada produjo resultados muy aproximados a la solución teórica, como puede verse de los resultados mostrados, esto pese a que la malla fue medianamente refinada. Podríamos concluir que para el caso axisimétrico los elementos SHELL producen resultados adecuados y confiables para los diseños.